Independent networks (Autonomous Systems, or ASes) engage in typically
voluntary bilateral interconnection ("peering") agreements
to provide reachability to each other for some subset of the Internet.
The implementation of these agreements introduces a non-trivial
set of constraints regarding paths over which Internet traffic can flow,
with implications for network operations, research, and evolution.
Realistic models of Internet topology, routing, workload, and performance
must account for the underlying economic dynamics. Although most
interconnection ("peering") agreements between networks are secret,
some information can be inferred from traceroute-derived and BGP-derived
Internet topology
data sets at IP, router, and AS granularities.
(For additional details on economic modeling, See our recently proposed
research on the economics of Internet transit and peering
interconnections.)
AS rank uses these data sets to estimate a macroscopic ranking of
Autonomous Systems based on a measure of their influence in the
global routing system, specifically the size of their customer cone
based on inferred business relationships among ASes. We explain these
concepts in more detail below.
An AS's rank is based on it's customer cone size, which in turn is
inferred from BGP paths by CAIDA's AS relationships inference algorithm9.
| num. ASNs | 10 | 9 | 9 | 8 | 3 | 2 |
| rank | 1 | 2 | 2 | 4 | 5 | 6 |
An AS's rank is equal to one greater than number of ASs with larger customer cone sizes
or degrees. So ASes with equally large customer cone sizes and degrees will
have the same rank. In such a case, the rank will increase by multiple steps
"after" a sequence of equally-ranked ASes.
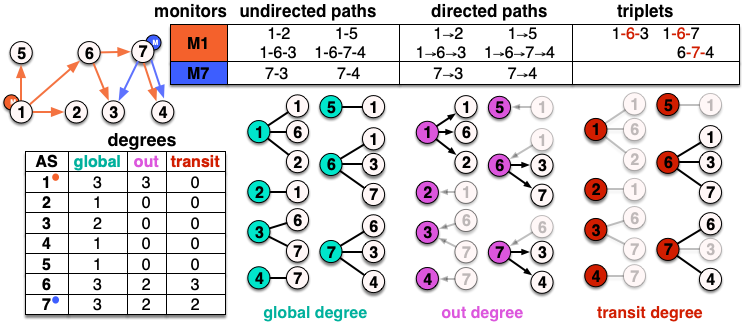
figure 1. Comparing the global degree, transit degree, and
outdegrees of ASes.
Degree is the number of neighbors that a node, an AS in our case, has in a graph. There are various types of degrees:
global, out, and transit. These degrees are applied to an unlabeled graph and so edge types are ignored.
Specifically, a global degree is a standard degree in which all of an AS's neighbors are counted. out and
transit degrees, however, change based on the observed paths. For example, out degree only counts neighbors that follow the
AS in the path and transit degree only counts neighbors that are found in at least one path where the AS is in between
that neighbor and another neighbor of the AS.
In Figure 1, ASes 2, 3, 4, and 5 have an outdegree of 0, since no nodes
follow them in any path. ASes 6 and 7, however, have an outdegree of 2,
while AS 1 has a high degree of 3 because it hosts a monitor.
If we consider a graph labeled with relationships, then there are additional
degree types such as siblings, customers, providers, and peers. An AS's sibling degree
is the number of neighbor ASes it shares from the same organizations. Customer,
provider, and peer degrees are the number of neighbors that are customers, providers,
and peers respectively.
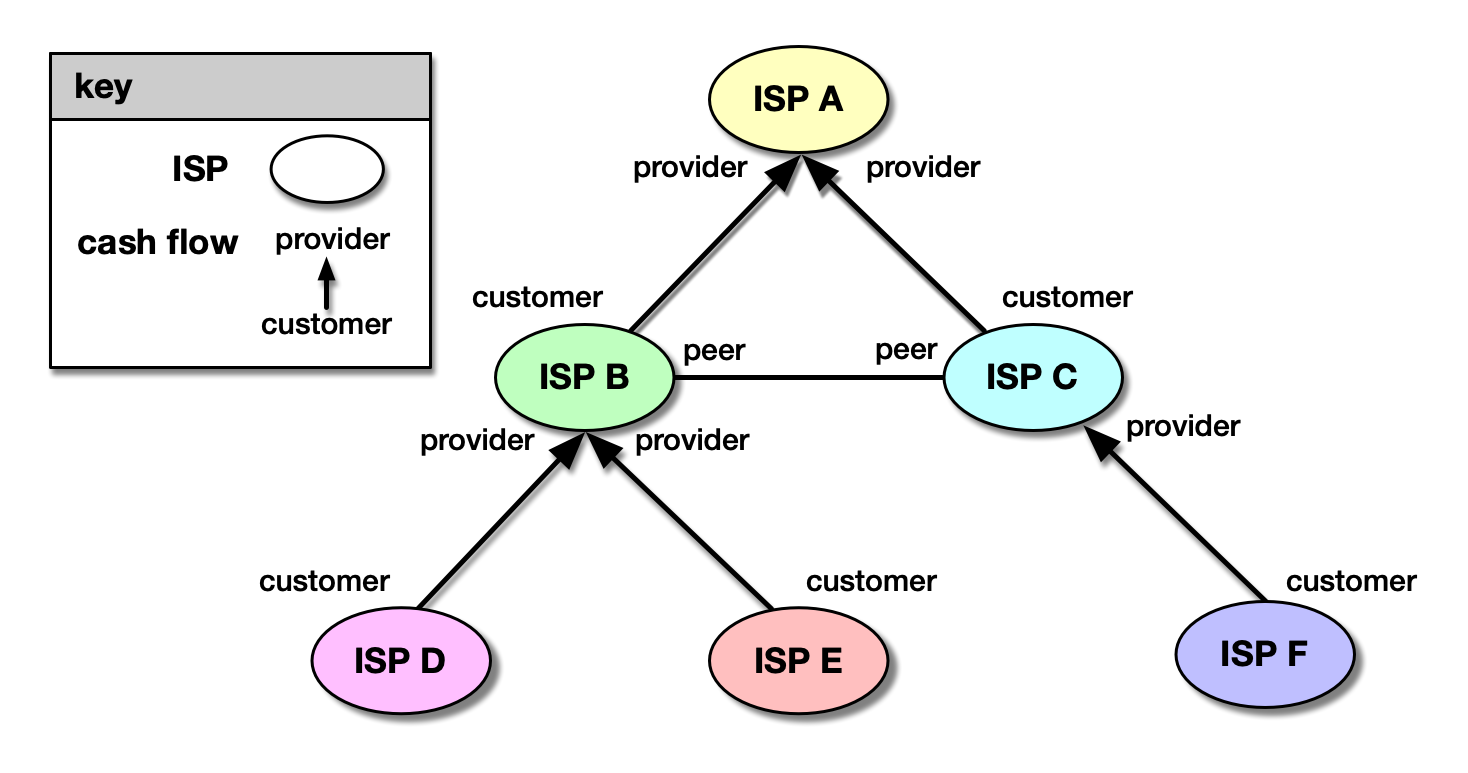
figure 2. Types of AS relationships. The ASes at the bottom of
the graph, D, E, and F, are customers of those above. ISPs in
the middle, B and C, are both providers of ASes below and
customers of ISPs above. ISPs B and C are also peers of each
other. ISP A at the top is a provider to B and C and a customer
of no one.
Background
Although business agreements between ISPs can be complicated, the original
model introduced by Gao 1 abstracts
business relationships into the following three most common types:
- customer-to-provider (c2p) (or if looked at from the opposite direction, provider-to-customer p2c),
- peer-to-peer (p2p), and
- sibling-to-sibling (s2s)
The justification for this classification is that an AS must buy
transit services for any traffic destined to parts of the Internet
that this AS neither owns nor can reach through its customers. In
Figure 2, arrow directions reflect flows of money -- ASes at
lower levels are customers who
pay ISPs (providers) at higher levels in exchange for
access to the rest of the Internet, also known as transit.
We refer to links between a customer and a provider as
c2p (p2c) links.
In Figure 2, D->B, E->B, F->C, B->A, and C->A are
c2p links.
A p2p link connects two ISPs who have
agreed to exchange traffic on a quid pro quo basis. Peers should exchange
traffic only between each other and each other's customers. Peering
allows growing ISPs to save money on transit costs they would
otherwise have to pay to deliver traffic to/from their customers.
In Figure 2, B-C is a p2p link, unidirectional since
neither B nor C pays the other for the traffic they exchange.
An s2s link connects two ASes
with a common administrative boundary. Such links usually
appear as a result of mergers and acquisitions, or under certain
network management scenarios.
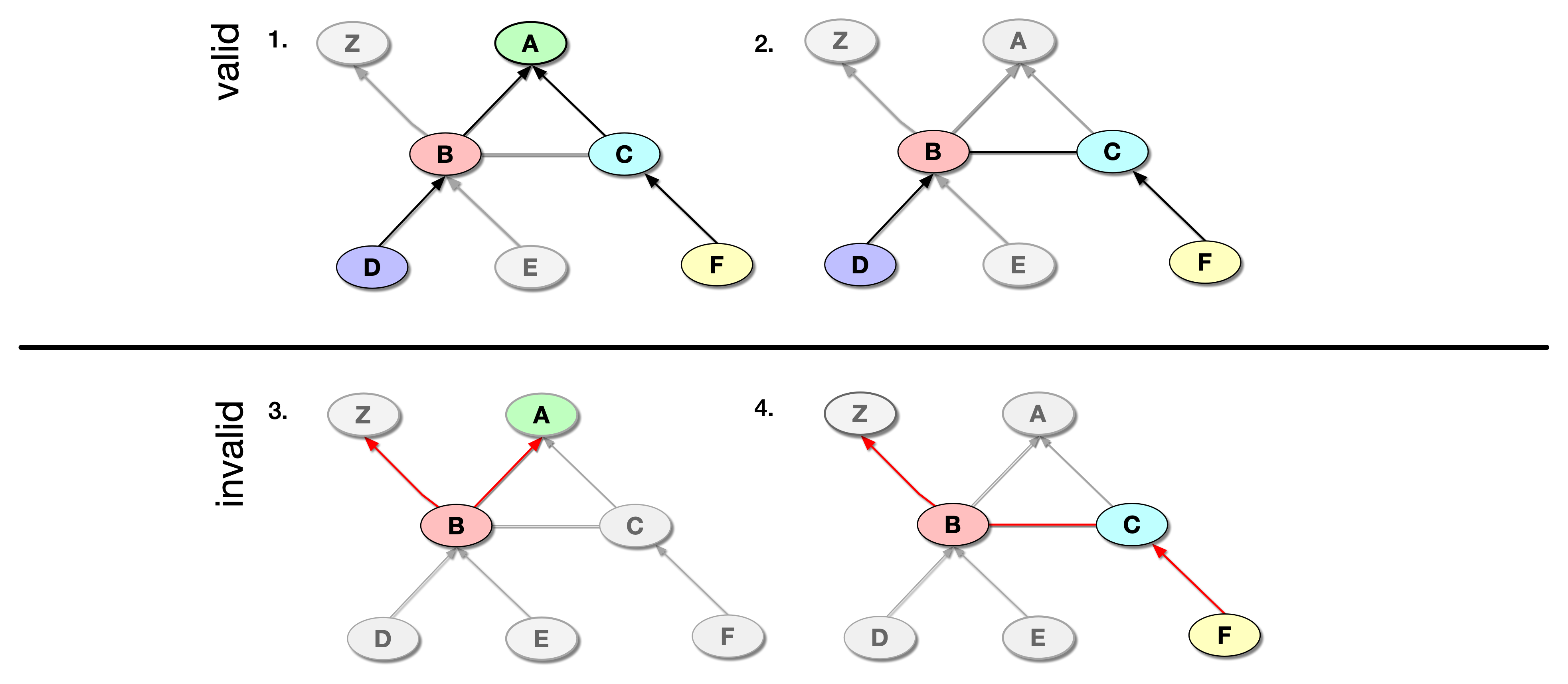
figure 3. The top two paths 1 and 2 are valid, while the bottom two
3 and 4 are invalid.
We use the notion of money transfers between ASes to define
valid and invalid
AS paths. A valid path between source
and destination ASes is one in which for every
ISP providing transit (a transit provider), there exists a customer
immediately adjacent to the ISP in the AS path.
An invalid path has at least one transit provider
not paid by a neighbor in the path.
In Figure 3 the top two examples are valid paths, while the bottom
two are invalid. In Example 1 the transit providers are A, B, and
C. ISPs B and C pay to A, D pays to B, and F pays to C. In Example
2 the transit providers are B and C, and they are paid by D and F,
respectively. In contrast, in Example 3 the transit provider is B,
but not only does no one pay B, but B itself pays both A and Z.
Example 4 also illustrates a situation where nobody pays transit
provider B.
In other words, a valid path must have the following
valid path pattern: zero or more c2p links,
followed by zero or one p2p link, followed by zero or more p2c
links. In addition, s2s links can appear in any number anywhere in
the path.
History of inference algorithms
Gao's1 pioneering work
inspired many researchers to seek
approaches to inferring ISP business relationships using information
from publicly available BGP routing tables. Gao used the concept
of valid paths as the basis for her inference heuristic and identified
the "top" provider in a given path based on AS degree (the number of
ASes with observed connectivity to a given AS).
Subramanian et al.2
provided a more elegant mathematical formulation based on the
concept of valid paths, but they simplified the problem by not
inferring s2s links. Using maximization of valid paths as an objective,
they formulated the AS relationship inference problem as a
combinatorial optimization problem: given an undirected
graph G derived from a set of BGP paths
P, assign the edge type (c2p or p2p)
to every edge in G such that the total
number of valid paths in P is maximized.
They called the problem the type-of-relationship (ToR) problem,
conjectured that it is NP-complete, and provided a heuristic solution.
Di Battista et al.3 and independently
Erlebach et al.4 proved that the
ToR problem is indeed NP-complete. The latter proved also that it is even
harder, APX-complete. More importantly for practical purposes, both
studies demonstrated that p2p links cannot
be inferred in the ToR problem formulation, and they developed mathematically
rigorous approximate solutions to the ToR problem but inferred
only c2p and p2c links. No technique thus far reliably identifies
p2p links.
Dimitropoulos, et al.6
identified still other issues with the ToR formulation, like the random
breaking of ties which can yield obviously incorrect inferences,
e.g., well-known large providers are inferred as customers
of small ASes. In the first paper6
we handled this issue with multiobjective optimization techniques
that incorporated AS degree into the inference. In a subsequent
paper7 we introduced improved
algorithms that determine not only c2p but also p2p links (for
those we can detect from BGP data). These improvements achieved
more accurate AS relationship inferences,
which we demonstrate against ground truth for a set of ASes.
Benjamin Hummel and Sven Kosub
8 introduced the idea that
the resulting graph should be acyclic, i.e. should contain no cycles,
and presented a new algorithm that does the assignment and reduces
the number of cycles. Our current technique creates no cycles,
but at the cost of ``valid'' (valley-free) paths in the graph.
M. Luckie et al.9 dropped the
valley-free assumption and instead
relied on three assumptions about the Internet's inter-domain structure:
(1) an AS enters into a provider relationship to become globally reachable;
and (2) there exists a peering clique of ASes at the top of the hierarchy,
and (3) there is no cycle of p2c links.
One metric of the resulting AS relationship graph that allows comparison
across ASes is the customer cone -- the set of ASes, IPv4
prefixes, or IPv4 addresses that can be
reached from a given AS following only customer links.
Looking specifically at the AS customer cone,
we define an AS A's AS customer cone
as the AS A itself plus all the ASes that can be reached
from A following only p2c links in BGP paths we observed.
In other words, A's customer cone contains A, plus A's
customers, plus its customers' customers, and so on.
Each AS announces a set of IPv4 prefixes. Each IPv4 prefix represents a
set of contiguous IPv4 addresses which are routed as a unit. Prefixes can
be nested, with the most specific prefix used for routing over less
specific prefixes. To find the set of prefixes which are reachable in
AS A's IPv4 prefix customer cone create the union of prefixe
announced by all ASes found in AS A's AS customer cone.
AS A's IPv4 address customer cone is the set of addresses
covered by AS A's IPv4 prefix customer cone.
Prefixes overlap, which represent a set of IPv4 addresses.
The size of the
customer cone of an AS reflects the number of other elements (ASes,
IPv4 prefixes, or IPv4 addresses) found in it's set. An AS in the customer
cone is assumed to pay, directly or indirectly, for transit, and provides a
coarse metric of the size or influence of an AS in the routing system.
Figure 4 depicts several AS customer cones, ASes D, E, F
, and I all sit at the bottom of the hierarchy
and so only have a single AS in their cone. H ranks
a little bit higher with 2 ASes. Both C and B
tie with 3 ASes. Note that B and C both have
E in their respective cones. A is ranked at the top
of the hierarchy with 6 ASes in its customer cone.
ASes with large customer cones play an important role
in the Internet's capital and governance structure. At the top of
this hierarchy are ISPs commonly known as Tier-1 ISPs, which
do not pay for transit to upstream providers at all; instead they
peer with each other to provide connectivity to all
destinations in the Internet. At the bottom of the hierarchy are
customer ASes who do not have their own customers and pay
providers to reach all destinations in the Internet.
We define peering cone size ratio as the ratio in
customer cone sizes of a pair of ASes if they (hypothetically) peered.
Similar customer cone sizes will have this ratio closer to 100,
also an indication the ASes have more incentive to peer.
The closer this ratio is to zero, the larger the difference in
customer cone sizes, and the less incentive the larger provider
will have to peer with the smaller.
If a given link (AS relationship) is currently a customer link
and changes to a peering link, then the provider-turned-peer's customer
cone will likely shrink, because the cone will lose any customer ASes
that the given AS used to access through that customer-turned-peer.
The customer-turned-peer's cone size will not change since the
provider-turned-peer is not included in the customer cone.
To compare magnitude of differences, the peering cone size ratio
always uses the larger customer cone as the denominator.
For example, for AS pair S and N, with customer cone sizes
C(S) and C(N), respectively , if C'(S) and C'(N) were
their respective customer cone sizes if S and N became
p2p peers (with other links unchanged),
then the peering cone size ratio is C'(N)/C'(S)
if C'(S) > C'(N), otherwise C'(S)/C'(N).
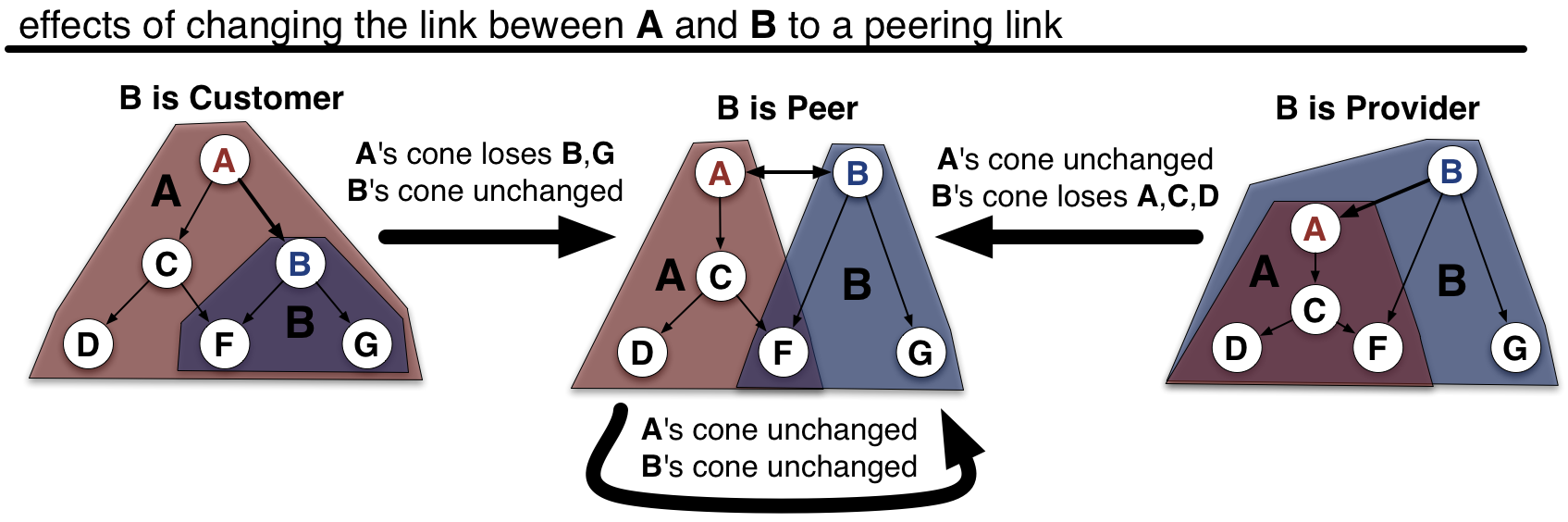 figure 5.
shows the effect on customer cones of changing the relationship of A to B
from its current one to a peering relationship.
figure 5.
shows the effect on customer cones of changing the relationship of A to B
from its current one to a peering relationship.
Figure 5 illustrates how different relationships affect the customer cone sizes
of AS A and B. If the original graph had B as a
customer of A then A's
cone contains 7 ASes: A,B,C,D,E,F,G. B's cone
contains three ASes:B,F,G. If the link between A and
B is changed to a peering link, A loses customers
B and G, which it had access to exclusively through
its customer relationship with B. A's cone does not
lose F, since it can still reach it through its customer
relationship with C. A's cone size thus shrinks to 4
ASes:A,C,D,F. Since AS B did not previously reach
any customers through A, its customer cone is unaffected by
this change.
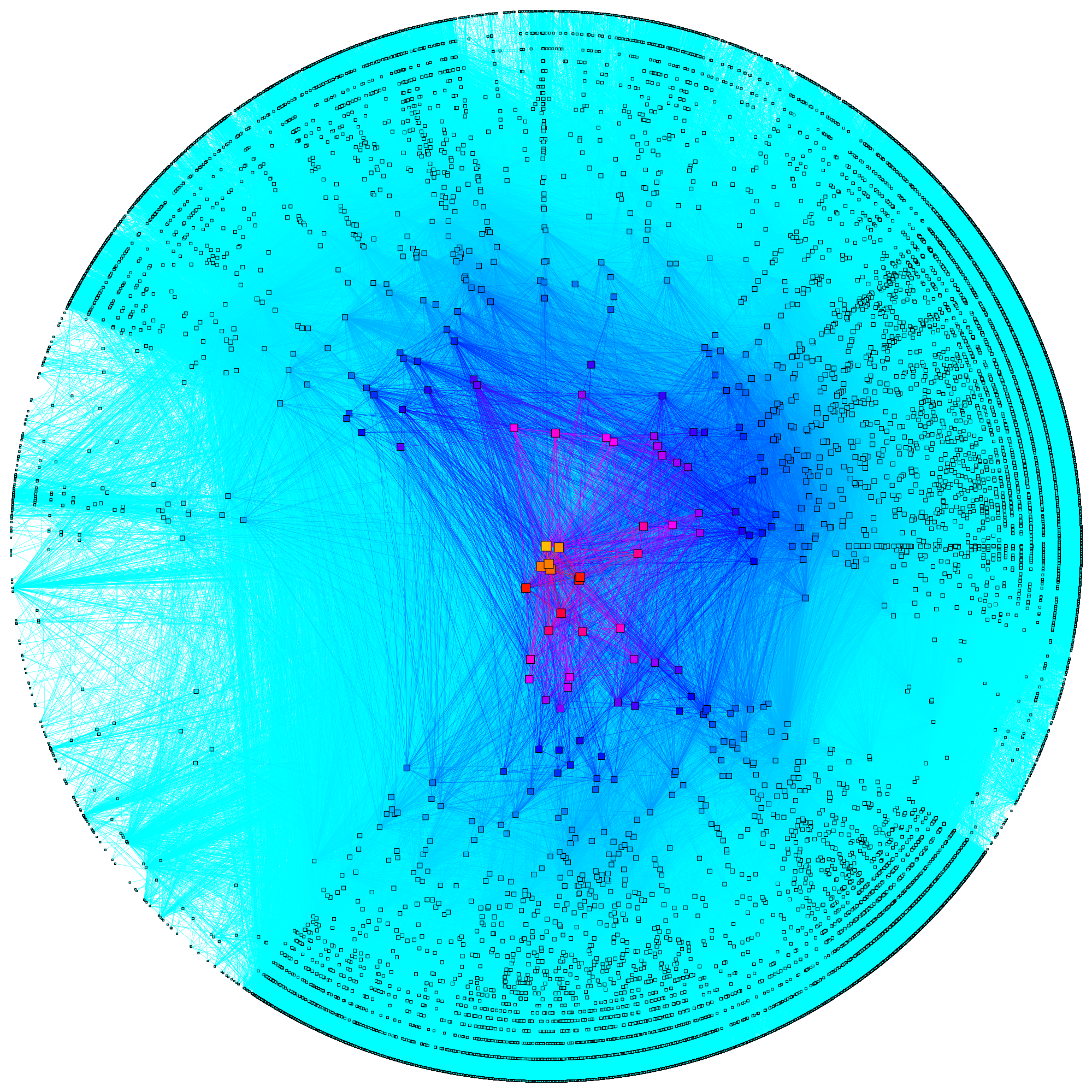 figure 6
figure 6 AS Core visualization.
figure 7 Coordinates of AS in AS core visualization.
The CAIDA AS Core visualization depicts the Internet's Autonomous Systems' (ASes) geographic locations, number of customers, and interconnections. Each AS approximately corresponds to an Internet Service Provider (ISP). The geographic location of the individual AS is inferred from the weighted centroid of its address space according to NetAcuity, a commercial geolocation service. The number of direct or indirect customers of an ASA is inferred using its customer cone (described below).
Each AS node is plotted in polar coordinates (radius, angle) on the circle, as formally defined in the equations below. The distance of each AS node from the center of the circle (the radial coordinate) is the inverse of each AS's customer cone size, (roughly) the number of the AS's direct or indirect customers. ASes at the outer edge of the circle have no customers and ASes at the center have the largest number of customers. The angular coordinate indicates the AS's geographic longitude.
Each AS is placed according to the longitude of the centroid of its announced address space. This is representative of the area where NetAcuity inters the majority of this network's activity occurs.
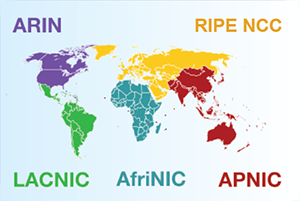 figure 7.
figure 7.The five Regional Internet Registries (RIRs).
 figure 8.
figure 8.AS Core by Regional Internet Registries.
The Regional Internet Registries (RIRs) manage allocation and registration of Internet number resources, such as AS numbers, within a particular region of the world. Although most ASes geolocate to the region of the originally allocating RIR, some multinational networks, e.g., AS3257 (Tinent) geolocate outside their region.
American Registry for Internet Numbers (ARIN) for the United States, Canada, several part of the Caribbean region, and Antarctica.
Reseaux IP Europeens Network Coordination Centre (RIPE NCC) for Europe, Russia, the Middle East, and Central Asia.
Latin America and Caribbean Network Information Centre (LACNIC) for Latin America and parts of the Caribbean region.
African Network Information Center (AFRINIC) for Africa.
Asia-Pacific Network Information Centre (APNIC) for Asia, Australia, New Zealand, and neighboring countries.
Although we know of no more rigorous empirical analysis of
macroscopic Internet topology enriched with AS relationships, we
recognize that resource limitations constrain the quality of the
science we can do.
-
AS relationships are more complex than allowed for in our approach.
The semantics of routing relationships between the same two ASes
can differ by peering location or even by prefix; our model
oversimplifies these cases by assigning a single relationship to
each pair of ASes.
-
A truly accurate picture of the Internet topology would require
collection of data from every AS, while our automated ranking
procedure is limited by the measurement data available to us.
-
We know of no more reliable heuristic for accurately inferring
peering relationships.
We are still seeking validation of these heuristics and their specific
parameters against ground truth from providers.
-
Our city-level visualization is limited by the accuracy of
IP address geolocation and our sampling only a subset of
a given AS's topology. Although the ITDK topology contains
exclusively router IP addresses (not end hosts), MaxMind's
GeoLite City
is optimized for geolocating end hosts and is likely less
accurate for router addresses. Although our
IPv4 Routed /24 Topology
measurements
exhaustively probe every routed /24, we do not capture the
full IPv4 topology, but a broad sample of paths from
monitors to target destinations, which results in a
sample of the underlying router topology.
In the future we would like to improve the
integrity and utility of the relationship-based AS ranking.
with more vantage points, more probing, cross-validation with
conjunction with other sources of data, and more powerful data
processing techniques to support larger topology samples.
- RouteViews is the project at
the University of Oregon that provides BGP routing data for AS Rank.
- Netacuity
(Digital Elements) is a commercial geolocation service
that we use to map ASes and their prefixes to geographic
locations.
- Organization:
this data comes from CAIDA's Inferred AS to Organization Mapping Dataset that maps mapping
Autonomous Systems (AS) to organizations
using quarterly bulk dumps of WHOIS databases. We use
this to provide names for ASes and their organizations, as well as
group ASes together that belong to the same organization.
- WHOIS information from the following Regional Internet Registries: ARIN, LACNIC, AFRINIC, APNIC, JPNIC, KRNIC, as well as RIPE NCC.
- AS
Relationships contains CAIDA's inferences about
AS
Relationships, Customer Cones, and Validation
using monthly BGP traces. We use it to infer each ASes'
links and their business types, degree, and customer cone.
@misc{caida_asrank,
Howpublished = {{path{http://as-rank.caida.org/}},
Month = {},
Title = {CAIDA AS Rank},
Year = {}
}
| 1 |
L. Gao,
On Inferring Autonomous System Relationships in
the Internet,
IEEE/ACM Transactions on Networking, December 2001.
|
| 2 |
L. Subramanian, S. Agarwal, J. Rexford, and R. H. Katz,
Characterizing the Internet Hierarchy from
Multiple Vantage
Points,
IEEE INFOCOM, 2002.
|
| 3 |
G. Di Battista, M. Patrignani, and M. Pizzonia,
Computing the Types of the Relationships between
Autonomous
Systems,
IEEE INFOCOM, 2003.
|
| 4 |
T. Erlebach, A. Hall, and T. Schank,
Classifying Customer-Provider Relationships in the
Internet,
Proceedings of the IASTED International Conference on
Communications and Computer Networks (CCN), 2002.
|
| 5 |
J. Xia and L. Gao,
On the Evaluation of AS Relationship
Inferences,
IEEE Globecom, 2004.
|
| 6 |
X. Dimitropoulos, D. Krioukov, B. Huffaker, kc claffy, and G.
Riley,
Inferring AS Relationships: Dead End or Lively
Beginning,
International Workshop on Efficient and Experimental Algorithms (WEA),
2005.
|
| 7 |
X. Dimitropoulos, D. Krioukov, M. Fomenkov, B. Huffaker, Y. Hyun,
kc claffy, and G. Riley,
AS Relationships: Inference and Validation,
ACM SIGCOMM Computer Communication Review (CCR), v.37, n.1, pp.29-40,
2007.
|
| 8 |
B. Hummel and S. Kosub
Acyclic Type-of-Relationship Problems on the
Internet: An Experimental Analysis ,
In Proceedings of the 7th ACM SIGCOMM Internet Measurement Conference
(IMC'2007), pages 221-226. ACM Press, New York, NY, 2007.
|
| 9 |
M. Luckie, B. Huffaker, k. claffy, A. Dhamdhere, and V. Giotsas,
AS Relationships, Customer Cones, and Validation
,
in Internet Measurement Conference (IMC), Oct 2013, pp. 243--256.
|